L'entropie à partir des premiers principes

1 janvier 2025

Je trouve l’entropie extrêmement fascinante. Cependant, faire le lien entre la formule $\sum p_{i} lo g \frac{1}{p _{i}}$ et ses explications “intuitives” concernant les codes préfixes et le contenu informationnel n’est pas évident. Ici, je souhaite passer en revue quelques manières d’aboutir indépendamment à cette idée.

Propriétés de l’information

Supposons que nous voulions définir une fonction $I$ , qui représente la quantité d’information d’un événement. En faisant abstraction des spécificités de l’événement, une mesure que nous pourrions utiliser pour comparer un événement à un autre est leur probabilité d’occurrence. Ainsi, $I$ pourrait être une application d’une probabilité $p \in [0, 1]$ vers $R$ . Avec ce cadre, les exigences suivantes sont raisonnables :

$I (1) = 0$ . Si un événement se produit certainement, il n’est pas très intéressant et nous donne peu d’information.
$I$ doit être continue et monotoniquement décroissante sur $[0, 1]$ . Un événement plus commun est moins informatif.
Deux événements indépendants de probabilités $p$ et $q$ doivent avoir une information $I (p) + I (q)$

La dernière exigence est la plus révélatrice. Par définition, la probabilité que deux événements indépendants se produisent est $pq$ . Donc

I (pq) = I (p) + I (q) .

Puisque la fonction doit être continue, cela n’est vrai que pour

I (p) = c lo g p .

Si nous voulons que $I$ soit monotoniquement décroissante,

\frac{d I}{d p} = c / p

doit être négative. Puisque $p$ est positif, $c$ doit être négatif. En posant $c^{'} = - c$

I (p) = c^{'} lo g \frac{1}{p}

Puisque $lo g_{a} b = \frac{l o g b}{l o g a}$ , où le dénominateur est une constante, nous pouvons considérer que $c^{'}$ encode la base du logarithme. Par commodité, nous posons $c^{'} = 1$ , et nous laissons $lo g$ désigner le logarithme en base 2.

L’entropie est simplement l’espérance de $I$ , sur une distribution $p = (p_{1}, p_{2}, \dots, p_{n})$

H (p) = i = 1 \sum n p_{i} lo g \frac{1}{p _{i}}

Nous supposons également que $H (0) = 0 lo g \frac{1}{0} = 0$ , ce qui est motivé par la continuité.

Par exemple, considérons la variable aléatoire de Bernoulli $B_{p}$ , qui prend la valeur $1$ avec une probabilité $p$ , et $0$ avec une probabilité $1 - p$ . Si nous traçons son entropie

Code de tracé

from pathlib import Path

import numpy as np
import plotly.graph_objects as go

# Function to calculate the entropy of a Bernoulli variable
def bernoulli_entropy(p):
    return -p * np.log2(p) - (1 - p) * np.log2(1 - p)

# Generate values for p from 0 to 1
p_values = np.linspace(0.01, 0.99, 100)
entropy_values = bernoulli_entropy(p_values)

# Shared trace for both themes
trace = go.Scatter(
    x=p_values,
    y=entropy_values,
    mode="lines",
    name="Entropy",
    line=dict(color="red"),
)

# Output directory (repo root/static)
output_dir = Path(__file__).resolve().parents[3] / "static"
output_dir.mkdir(parents=True, exist_ok=True)

themes = [
    {
        "template": "plotly_white",
        "font_color": "#111111",
        "axis": {
            "linecolor": "#111111",
            "tickcolor": "#111111",
            "tickfont": {"color": "#111111"},
            "title_font": {"color": "#111111"},
            "showgrid": True,
            "gridcolor": "rgba(17, 17, 17, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_light.html",
    },
    {
        "template": "plotly_dark",
        "font_color": "#f5f5f5",
        "axis": {
            "linecolor": "#f5f5f5",
            "tickcolor": "#f5f5f5",
            "tickfont": {"color": "#f5f5f5"},
            "title_font": {"color": "#f5f5f5"},
            "showgrid": True,
            "gridcolor": "rgba(245, 245, 245, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_dark.html",
    },
]

for theme in themes:
    fig = go.Figure(data=[trace])
    fig.update_layout(
        title="Entropy of a Bernoulli Random Variable",
        xaxis_title="p",
        yaxis_title="Entropy",
        template=theme["template"],
        font=dict(color=theme["font_color"]),
        paper_bgcolor="rgba(0, 0, 0, 0)",
        plot_bgcolor="rgba(0, 0, 0, 0)",
        xaxis=dict(showline=True, **theme["axis"]),
        yaxis=dict(showline=True, **theme["axis"]),
    )
    fig.write_html(output_dir / theme["filename"])

nous voyons qu’elle est maximisée lorsque la distribution est uniforme, et minimisée lorsqu’elle est presque déterministe.

Codes préfixes

Supposons que nous ayons un ensemble de symboles $X = {X_{1}, \dots, X_{M}}$ que nous souhaitons transmettre sur un canal binaire. Nous concevons le canal de manière à pouvoir envoyer un $1$ ou un $0$ à la fois. Nous voulons trouver un schéma de codage optimal pour $X$ , avec une exigence : il doit être préfixe.

Définissons une fonction de codage $f : X \to {0, 1}^{+}$ , qui associe les symboles à des chaînes binaires de longueur $\geq 1$ . Nous disons qu’un codage est préfixe si aucun mot de code n’est le préfixe d’un autre. Par exemple, ${0, 01}$ n’est pas préfixe car $0$ est un préfixe de $01$ . En revanche, ${0, 10}$ l’est.

Un code préfixe implique que le code est uniquement déchiffrable sans délimiteurs supplémentaires entre les symboles, ce qui est une propriété souhaitable.

Nous remarquons également qu’un code binaire préfixe est uniquement défini par un arbre binaire :

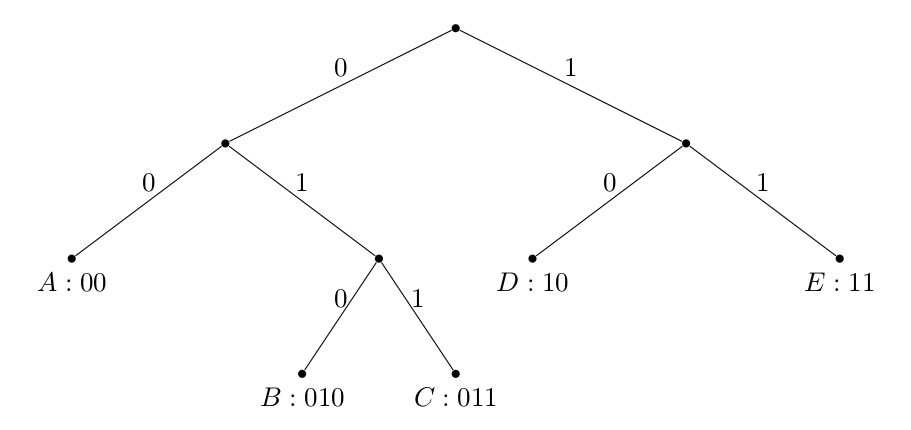
Arbre binaire d’un code préfixe — Source : https://leimao.github.io/blog/Huffman-Coding

où le chemin de la racine au symbole détermine le mot de code, et les symboles sont toujours des feuilles. Assurez-vous que toute construction de ce type produit un code préfixe.

Nous allons maintenant montrer que la longueur moyenne d’un mot de code $L$ de tout code préfixe sur $X$ est bornée par

H (X) \leq L < H (X) + 1.

où $X$ est une variable aléatoire prenant des valeurs dans l’ensemble $X$ avec des probabilités $(p_{1}, \dots, p_{n})$ . Plus important encore, nous voyons que l’entropie de $X$ est une limite inférieure pour le degré de compression d’une distribution, ou de manière équivalente, pour la quantité d’information qu’elle contient.

Inégalité de Kraft

Supposons que $l_{i}$ soit la longueur du $i$ ème mot de code. Si le code est préfixe :

i = 1 \sum M 2^{- l_{i}} \leq 1

Preuve :

Soit $l_{max}$ la longueur du mot de code le plus long. On remarque que :

Il y a au plus $2^{l_{max}}$ nœuds au niveau $l_{max}$
Pour tout mot de code de longueur $l_{i}$ , il y a $2^{l_{max} - l_{i}}$ descendants au niveau $l_{max}$ .
Les ensembles de descendants de chaque mot de code sont disjoints (puisqu’un mot de code n’est jamais le descendant d’un autre)

Cela implique

⟹ i \sum 2^{l_{max} - l_{i}} \leq 2^{l_{max}} i \sum 2^{- l_{i}} \leq 1.

Pourquoi $\leq$ au lieu de l’égalité ? Parce qu’il est possible qu’un nœud au niveau $l_{max}$ ne soit le descendant d’aucun mot de code (considérez l’arbre du code ${10, 11}$ ) !

Borne inférieure pour L

Maintenant, considérons la longueur moyenne d’un mot de code

L = i \sum p_{i} l_{i}

Nous allons montrer que l’entropie est une borne inférieure pour $L$ , soit

H (X) \leq L ⟺ L - H (X) \geq 0

Démonstration :

L - H (X) = i \sum p_{i} l_{i} + i \sum p_{i} lo g p_{i} = - i \sum p_{i} lo g 2^{- l_{i}} + i \sum p_{i} lo g p_{i} = - i \sum p_{i} lo g 2^{- l_{i}} + i \sum p_{i} lo g p_{i} + i \sum p_{i} lo g (j \sum 2^{- l_{j}}) - i \sum p_{i} lo g (j \sum 2^{- l_{j}}) = i \sum p_{i} lo g \frac{p _{i}}{2 ^{- l_{i}} / \sum _{j} 2 ^{- l_{j}}} - i \sum p_{i} lo g (j \sum 2^{- l_{j}}) = D_{K L} [p ∣∣ q] + lo g \frac{1}{c} \geq 0

Où l’inégalité finale est due à 1) la divergence KL étant non négative et 2) à $c \leq 1$ en raison de l’inégalité de Kraft. Une chose à noter est que si $l_{i} = - lo g p_{i}$ , alors $L = H (X)$ , le minimum théorique. La raison pour laquelle nous ne pouvons pas toujours l’atteindre est que $- lo g p_{i}$ n’est pas nécessairement un entier, ce qui est évidemment requis.

Une borne supérieure pour L

Remarquez qu’il est possible de construire un code préfixe avec des longueurs

l_{i} = ⌈ - lo g p_{i} ⌉

puisqu’elles satisfont l’inégalité de Kraft :

i \sum 2^{- l_{i}} \leq i \sum 2^{l o g p_{i}} = 1

Par la définition de la fonction plafond

- lo g p_{i} \leq l_{i} < - lo g p_{i} + 1

En prenant l’espérance sur $p$ , on obtient

- \sum p_{i} lo g p_{i} \leq \sum p_{i} l_{i} < - \sum p_{i} lo g p_{i} + 1 ⟹ H (X) \leq L < H (X) + 1

Cela montre que $H (X) + 1$ est une bonne borne supérieure pour L !

En résumé, l’entropie est une borne inférieure, et une estimation raisonnable, pour le nombre moyen de bits nécessaires pour encoder une distribution sous forme de code préfixe.

Références

Cours ECE 255A d’Alon Orlitsky, UCSD
Cover, T. M., & Thomas, J. A. (2006). Éléments de théorie de l’information. Wiley-Interscience.

←

Modèles de Mélange Gaussien Interactifs