熵的第一性原理解释

2025年1月1日

我发现熵这个概念极其迷人。但将公式 $\sum p_{i} lo g \frac{1}{p _{i}}$ 与其关于前缀码和信息量的"直观"解释对应起来并不容易。在此，我想探讨几种独立推导出这一概念的思路。

信息量的性质

假设我们想要定义一个函数 $I$ ，用于表示事件的信息量。抛开事件的具体细节，我们可以使用一种度量来比较不同事件，即它们发生的概率。因此， $I$ 可以是从概率 $p \in [0, 1]$ 到 $R$ 的映射。基于此框架，以下要求是合理的：

$I (1) = 0$ 。如果一个事件必然发生，它就不太有趣，提供的信息量也很少。
$I$ 应在 $[0, 1]$ 上连续且单调递减。越常见的事件信息量越少。
两个独立事件，其概率分别为 $p$ 和 $q$ ，它们的信息量应为 $I (p) + I (q)$

最后一条要求最能说明问题。根据定义，两个独立事件同时发生的概率是 $pq$ 。因此

I (pq) = I (p) + I (q) .

由于函数必须是连续的，这仅当

I (p) = c lo g p .

时成立。

如果我们希望 $I$ 单调递减，则

\frac{d I}{d p} = c / p

必须为负。由于 $p$ 为正， $c$ 必须为负。令 $c^{'} = - c$

I (p) = c^{'} lo g \frac{1}{p}

由于 $lo g_{a} b = \frac{l o g b}{l o g a}$ ，其中分母为常数，我们可以将 $c^{'}$ 视为对数的底数编码。为方便起见，我们令 $c^{'}$ 为 1，并令 $lo g$ 表示以 2 为底的对数。

熵就是 $I$ 在分布 $p = (p_{1}, p_{2}, \dots, p_{n})$ 上的期望值

H (p) = i = 1 \sum n p_{i} lo g \frac{1}{p _{i}}

我们同样假设 $H (0) = 0 lo g \frac{1}{0} = 0$ ，这是出于连续性的考虑。

例如，考虑伯努利随机变量 $B_{p}$ ，它以概率 $p$ 取值 $1$ ，以概率 $1 - p$ 取值 $0$ 。如果我们绘制其熵图

绘图代码

from pathlib import Path

import numpy as np
import plotly.graph_objects as go

# Function to calculate the entropy of a Bernoulli variable
def bernoulli_entropy(p):
    return -p * np.log2(p) - (1 - p) * np.log2(1 - p)

# Generate values for p from 0 to 1
p_values = np.linspace(0.01, 0.99, 100)
entropy_values = bernoulli_entropy(p_values)

# Shared trace for both themes
trace = go.Scatter(
    x=p_values,
    y=entropy_values,
    mode="lines",
    name="Entropy",
    line=dict(color="red"),
)

# Output directory (repo root/static)
output_dir = Path(__file__).resolve().parents[3] / "static"
output_dir.mkdir(parents=True, exist_ok=True)

themes = [
    {
        "template": "plotly_white",
        "font_color": "#111111",
        "axis": {
            "linecolor": "#111111",
            "tickcolor": "#111111",
            "tickfont": {"color": "#111111"},
            "title_font": {"color": "#111111"},
            "showgrid": True,
            "gridcolor": "rgba(17, 17, 17, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_light.html",
    },
    {
        "template": "plotly_dark",
        "font_color": "#f5f5f5",
        "axis": {
            "linecolor": "#f5f5f5",
            "tickcolor": "#f5f5f5",
            "tickfont": {"color": "#f5f5f5"},
            "title_font": {"color": "#f5f5f5"},
            "showgrid": True,
            "gridcolor": "rgba(245, 245, 245, 0.2)",
            "gridwidth": 1,
            "zeroline": False,
        },
        "filename": "bernoulli_entropy_plot_dark.html",
    },
]

for theme in themes:
    fig = go.Figure(data=[trace])
    fig.update_layout(
        title="Entropy of a Bernoulli Random Variable",
        xaxis_title="p",
        yaxis_title="Entropy",
        template=theme["template"],
        font=dict(color=theme["font_color"]),
        paper_bgcolor="rgba(0, 0, 0, 0)",
        plot_bgcolor="rgba(0, 0, 0, 0)",
        xaxis=dict(showline=True, **theme["axis"]),
        yaxis=dict(showline=True, **theme["axis"]),
    )
    fig.write_html(output_dir / theme["filename"])

我们可以看到，当分布均匀时熵最大，而当分布几乎确定时熵最小。

前缀无关码

假设我们有一组符号 $X = {X_{1}, \dots, X_{M}}$ 需要通过二进制信道传输。我们构建的信道要求每次只能发送 $1$ 或 $0$ 。我们希望为 $X$ 找到最优编码方案，但有一个要求：它必须是前缀无关的。

定义编码函数 $f : X \to {0, 1}^{+}$ ，它将符号映射到长度 $\geq 1$ 的二进制字符串。如果没有任何码字是另一个码字的前缀，我们就称该编码是前缀无关的。例如 ${0, 01}$ 不是前缀无关码，因为 $0$ 是 $01$ 的前缀；而 ${0, 10}$ 则是。

前缀无关码意味着该编码具有唯一可解码性，无需在符号间添加额外分隔符，这是一个理想特性。

我们还注意到，二进制前缀码可以通过二叉树唯一确定：

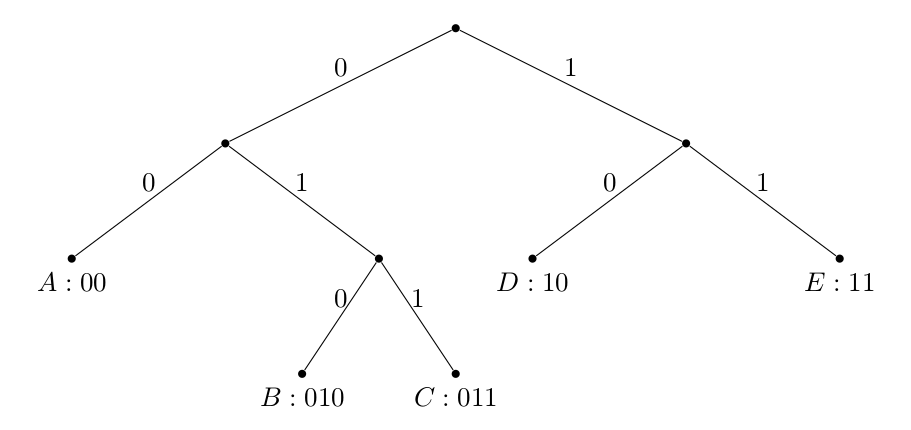
前缀码的二叉树结构 — 来源：https://leimao.github.io/blog/Huffman-Coding

其中从根节点到符号的路径决定了码字，且符号始终位于叶节点。请自行验证：任何此类构造都会产生前缀无关码。

现在我们将证明，任意前缀码在 $X$ 上的期望码长 $L$ 满足以下界限：

H (X) \leq L < H (X) + 1.

其中 $X$ 是取值于集合 $X$ 的随机变量，其概率分布为 $(p_{1}, \dots, p_{n})$ 。最重要的是，我们观察到 $X$ 的熵是该分布可压缩程度的下界，或者说它包含的信息量的下界。

克拉夫特不等式

假设 $l_{i}$ 是第 $i$ 个码字的长度。如果该编码是前缀无关的：

i = 1 \sum M 2^{- l_{i}} \leq 1

证明：

令 $l_{max}$ 为最长码字的长度。我们注意到：

在第 $l_{max}$ 层最多有 $2^{l_{max}}$ 个节点
对于任意长度为 $l_{i}$ 的码字，在第 $l_{max}$ 层有 $2^{l_{max} - l_{i}}$ 个后代节点
每个码字的后代节点集合互不相交（因为一个码字永远不会是另一个码字的祖先）

这些事实意味着

⟹ i \sum 2^{l_{max} - l_{i}} \leq 2^{l_{max}} i \sum 2^{- l_{i}} \leq 1.

为什么是 $\leq$ 而不是等号？因为有可能第 $l_{max}$ 层的某个节点不是任何码字的后代（考虑编码 ${10, 11}$ 对应的树）！

L 的下界

现在，我们来考虑期望码字长度

L = i \sum p_{i} l_{i}

我们将证明熵是 $L$ 的一个下界，即

H (X) \leq L ⟺ L - H (X) \geq 0

证明：

L - H (X) = i \sum p_{i} l_{i} + i \sum p_{i} lo g p_{i} = - i \sum p_{i} lo g 2^{- l_{i}} + i \sum p_{i} lo g p_{i} = - i \sum p_{i} lo g 2^{- l_{i}} + i \sum p_{i} lo g p_{i} + i \sum p_{i} lo g (j \sum 2^{- l_{j}}) - i \sum p_{i} lo g (j \sum 2^{- l_{j}}) = i \sum p_{i} lo g \frac{p _{i}}{2 ^{- l_{i}} / \sum _{j} 2 ^{- l_{j}}} - i \sum p_{i} lo g (j \sum 2^{- l_{j}}) = D_{K L} [p ∣∣ q] + lo g \frac{1}{c} \geq 0

其中最终的不等式成立是由于 1) KL 散度非负，以及 2) 根据 Kraft 不等式有 $c \leq 1$ 。需要注意的一点是，如果 $l_{i} = - lo g p_{i}$ ，则 $L = H (X)$ ，即理论最小值。我们无法总是达到此值的原因在于 $- lo g p_{i}$ 不一定为整数，而这显然是必需的条件。

L 的上界

注意到我们可以构建一个码长为

l_{i} = ⌈ - lo g p_{i} ⌉

的前缀码，因为它们满足克拉夫特不等式：

i \sum 2^{- l_{i}} \leq i \sum 2^{l o g p_{i}} = 1

根据向上取整函数的定义

- lo g p_{i} \leq l_{i} < - lo g p_{i} + 1

对 $p$ 取数学期望，我们得到

- \sum p_{i} lo g p_{i} \leq \sum p_{i} l_{i} < - \sum p_{i} lo g p_{i} + 1 ⟹ H (X) \leq L < H (X) + 1

这表明 $H (X) + 1$ 是 L 的一个良好上界！

总之，熵是使用前缀码编码分布时所需平均比特数的下界，也是一个合理的估计值。

参考文献

Alon Orlitsky 在加州大学圣地亚哥分校的 ECE 255A 课程讲座
Cover, T. M., & Thomas, J. A. (2006). 信息论基础. Wiley-Interscience.

←

交互式高斯混合模型